logistic回归又称logistic回归分析，是一种广义的线性回归分析模型，常用于数据挖掘，疾病自动诊断，经济预测等领域。 逻辑回归根据给定的自变量数据集来估计事件的发生概率，由于结果是一个概率，因此因变量的范围在 0 和 1 之间。

  逻辑回归不是一个回归的算法，逻辑回归是一个分类的算法。
  logistic回归是一种广义线性回归（generalized linear model），因此与多重线性回归分析有很多相同之处。它们的模型形式基本上相同，都具有w'x+b，其中w和b是待求参数，其区别在于他们的因变量不同，多重线性回归直接将w'x+b作为因变量，即y=w'x+b，而logistic回归则通过函数L将w'x+b对应一个隐状态p，p=L(w'x+b),然后根据p 与1-p的大小决定因变量的值。如果L是logistic函数，就是logistic回归，如果L是多项式函数就是多项式回归。
  logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释，多类可以使用softmax方法进行处理。实际中最为常用的就是二分类的logistic回归。

• sigmoid函数

# sigmoid函数

import numpy
import math
import matplotlib.pyplot as plt

def sigmoid(x):
    a=[]
    for item in x:
        a.append(1.0/(1.0+math.exp(-item)))
    return a

x = numpy.arange(-10,10,0.1)
y = sigmoid(x)

plt.plot(x,y)
plt.show()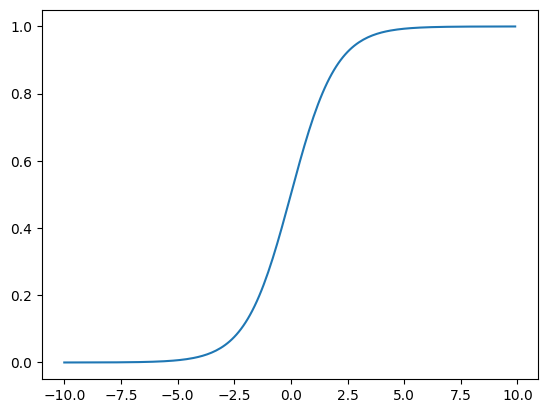

• 逻辑回归模型推导
• 逻辑回归损失函数的计算

似然函数：

L(\theta )=\prod_{i=1}^{m} (h_{\theta }(x^{(i)}))^{y^{(i)}}(1-h_{\theta }(x^{(i)}))^{1-y^{(i)}}

取对数：

l(\theta )=\log_{}{L(\theta)}=\sum_{i=1}^{m} y^{(i)}\log_{}{h(x^{(i)})} +(1-y^{(i)})\log_{}{(1-h(x^{(i)}))}

损失函数（加负号）：

J(\theta)=-[\sum_{i=1}^{m} y^{(i)}\log_{}{h(x^{(i)})} +(1-y^{(i)})\log_{}{(1-h(x^{(i)}))}]