梯度下降法（最好的无约束最优化问题的求解算法）

  梯度下降法(Gradient Descent)是一个算法，但不是像多元线性回归那样是一个具体做回归任务的算法，而是一个非常通用的优化算法来帮助一些机器学习算法求解出最优解的，所谓的通用就是很多机器学习算法都是用它，甚至深度学习也是用它来求解最优解。所有优化算法的目的都是期望以最快的速度把模型参数θ求解出来，梯度下降法就是一种经典常用的优化算法。

• 梯度下降法思想

  其实这就跟生活中的情形很像，比如你问一个朋友的工资是多少，他说你猜？然后你会觉得很难猜，他说你猜完我告诉你是猜高了还是猜低了，这样你就可以奔着对的方向一直猜下去，最后总有一下你能猜对。梯度下降法就是这样的，你得去试很多次，而且是不是我们在试的过程中还得想办法知道是不是在猜对的路上，说白了就是得到正确的反馈再调整然后继续猜才有意义。
  一般你玩儿这样的游戏的时候，一开始第一下都是随机瞎猜一个对吧，那对于计算机来说是不是就是随机取值，也就是说你有\theta=W_{1},...,W_{n}，这里\theta强调一下不是一个值，而是一个向量就是一组 W，一开始的时候我们通过随机把每个值都给它随机出来。有了\theta我们可以去根据算法就是公式去计算出来\hat {y}，比如\hat {y} =X\theta，然后根据计算\hat {y}和真实y之间的损失比如MSE，然后调整\theta再去计算MSE。
  这个调整正如咱们前面说的肯定不是瞎调整，当然这个调整的方式很多，你可以整体\theta每个值调大一点，也可以整体\theta每个值调小一点，也可以一部分调大一部分调小。第一次\theta _{0}我们可以得到第一次的MSE就是Loss_{0}，调整后第二次\theta _{1}对应可以得到第二次的MSE就是Loss_{}，如果loss变小是不是调对了，就应该继续调，如果 loss 反而变大是不是调反了，就应该反过来调。直到MSE我们找到最小值时计算出来的\hat\theta就是我们的最优解。
  这个就好比道士下山，我们把 loss 看出是曲线就是山谷，如果走过来就再往回调，所以是一个迭代的过程。

  这里梯度下降法的公式就是一个式子指导计算机迭代过程中如何去调整θ，不需要推导和证明，就是总结出来的:

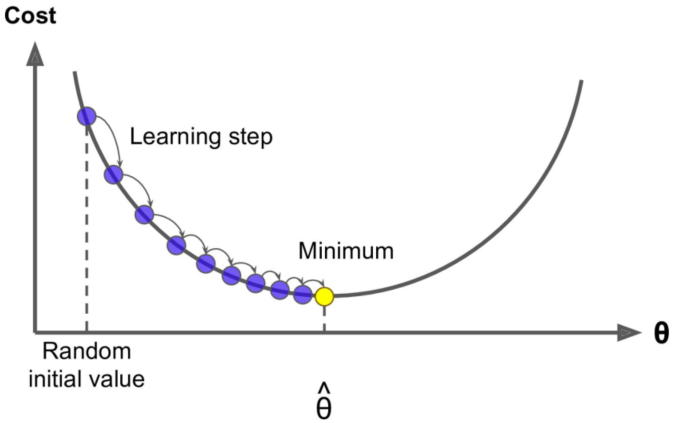
W_{j}^{t+1}=W_{j}^{t}-\eta \cdot gradient_{j}

这里的W_{j}就是\theta中的某一个j=0…n，这里的\eta就是图里的 learning step，很多时候也叫学习率 learning rate，很多时候也用\alpha表示，这个学习率我们可以看作是下山迈的步子的大小，步子迈的大下山就快。
  学习率一般都是正数，那么在山左侧梯度是负的，那么这个负号就会把W往大了调，如果在山右侧梯度就是正的，那么负号就会把W往小了调。每次W_{j} 调整的幅度就是\eta \cdot gradient_{j}，就是横轴上移动的距离。
  如果特征或维度越多，那么这个公式用的次数就越多，也就是每次迭代要应用的这个式子 n+1 次，所以其实上面的图不是特别准，因为θ对应的是很多维度，应该每一个维度都可以画一个这样的图，或者是一个多维空间的图。

• 学习率设置的学问

  根据我们上面讲的梯度下降法公式，我们知道η是学习率，设置大的学习率W_{j} 每次调整的幅度就大，设置小的学习率W_{j}每次调整的幅度就小，然而如果步子迈的太大也会有问题其实，俗话说步子大了容易扯着蛋，可能一下子迈到山另一头去了，然后一步又迈回来了，使得来来回回震荡。步子太小呢就一步步往前挪，也会使得整体迭代次数增加。

  学习率的设置是门学问，一般我们会把它设置成一个比较小的正整数，0.1、0.01、0.001、0.0001，都是常见的设定数值，一般情况下学习率在整体迭代过程中是一直不变的数，但是也可以设置成随着迭代次数增多学习率逐渐变小，因为越靠近山谷我们就可以步子迈小点，省得走过，还有一些深度学习的优化算法会自己控制调整学习率这个值。
  如果损失函数是非凸函数，梯度下降法是有可能落到局部最小值的，所以其实步长不能设置的太小太稳健，那样就很容易落入局部最优解，虽说局部最小值也没大问题，因为模型只要是堪用的就好嘛，但是我们肯定还是尽量要奔着全局最优解去。

• 梯度下降法流程

梯度下降法几步流程就是猜正确答案的过程：

1. 瞎蒙，Random随机\theta，随机一组数值W_{0}...W_{n}
2. 求梯度，为什么是梯度？因为梯度代表曲线某点上的切线的斜率，沿着切线往下下降就相当于沿着坡度最陡峭的方向下降
3. 如果梯度g<0,\theta变大，如果g>0,\theta变小
4. 判断是否收敛 convergence，如果收敛跳出迭代，如果没有达到收敛，回第 2 步继续

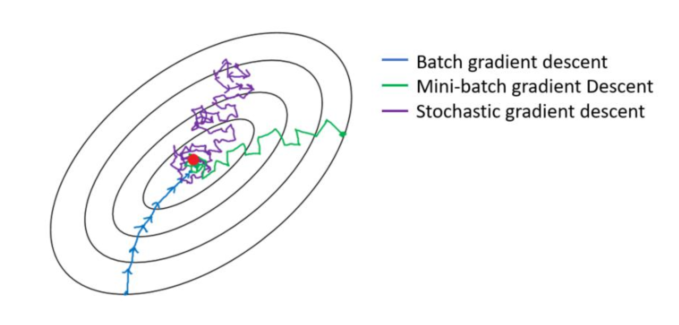
• 三种梯度下降法

1. 全量梯度下降 Batch Gradient Descent
2. 随机梯度下降 Stochastic Gradient Descent
3. 小批量梯度下降 Mini-Batch Gradient Descent
   
   区别：其实三种梯度下降的区别仅在于第2步求梯度所用到的X数据集的样本数量不同！它们每次学习(更新模型参数)使用的样本个数，每次更新使用不同的样本会导致每次学习的准确性和学习时间不同。

• 轮次和批次
  轮次：epoch，轮次顾名思义是把我们已有的训练集数据学习多少轮
  批次：batch，批次这里指的的我们已有的训练集数据比较多的时候，一轮要学习太多数据，那就把一轮次要学习的数据分成多个批次，一批一批数据的学习。

  举个例子，这就好比有一本唐诗 300 首需要大家背诵，如果要给你一周时间要你背诵完，或许你很聪明可以背完，但是估计也不敢说一下子全都记得特别牢，甚至到可以出口成章的地步吧。那通常人是怎么做的呢？是不是就是接下来多花几周，重复之前一周的动作，把 300 首唐诗多背几次，比如花 10 周把 300 首唐诗全部倒背如流了，然后又花了 10 周时间把 300 首唐诗又背诵到了滚瓜烂熟的地步终于可以出口成唐诗了。那么刚提到的 10 周、又 10 周放在 AI 领域那么就是所谓的训练了 10 个轮次又 10 个轮次，总共 20 个轮次。

  再回顾上面一段话，我们假设你很聪明，也就是 AI 训练的电脑性能处理能力非常好，如果是普通人或者一般的电脑，很有可能一周都不可能背诵完 300 首，也就是内存一下子装不下那么大的数据量，或者处理器计算能力没有那么快。当数据量大的情况下，这是很常见的现在，那么为了可以顺利背下来 300 首唐诗到举一反三出口成章的地方，也就是为了训练出来 model 模型，我们只能把一个轮次需要的数据分成多个批次来一点点计算，放到背唐诗的例子中，说白了就是一周背不下来 300 首唐诗，那么我们就一周背 50 首唐诗吧比如说，这样我们就需要 6 个批次把一轮数据背完，一个批次所需要的数据 batch_size 就是50。

  还有就是对于三种梯度下降来说，全量梯度下降就是每一轮次用到全量的数据，然后一次迭代就是一个轮次，然后用全量数据计算梯度来更新一下 W。随机梯度下降每一个轮次也需要计算所有数据，但是有多少数据就会分为多少个批次，即是一个批次一次迭代，就只用一条数据计算梯度来更新一下 W，所以随机梯度下降一个轮次中的更新 W 的次数等于样本总数。最后就是 mini-batch 梯度下降，每一个轮次也需要计算所有数据，但是轮次分成多 少 个 批 次 取 决 于 batch_size ， batch_size 大 需 要 的 轮 次 就 少 ， 比 如batch_size=num_samples，那就等价于全量批量梯度下降，batch_size=1 那就等价于随机梯度下降。

• 代码实现梯度下降法

1. 全量梯度下降

import numpy as np

# 创建数据集 X、y
np.random.seed(1)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
X_b = np.c_[np.ones((100, 1)), X]

# 创建超参数
learning_rate = 0.001
n_iterations = 10000

# 1，初始化 theta，w0...wn，正太分布创建 W
theta = np.random.randn(2, 1)

# 4，不会设置阈值，直接设置超参数，迭代次数，迭代次数到了，我们就认为收敛了
for _ in range(n_iterations):
  # 2，接着求梯度 gradient
  gradients = X_b.T.dot(X_b.dot(theta)-y)

  # 3，应用公式调整 theta 值，theta_t + 1 = theta_t - grad * learning_rate
  theta = theta - learning_rate * gradients

print(theta)
# 上面代码值得一提的是，X_b.T是X的转置，也就是n行m 列的矩阵，然后(X_b.dot(theta)-y)是
# 一个 m 行 1 列的列向量，这样矩阵乘以向量会得到一个 n 行一列的列向量，相当于一下子计算
# 出来所有维度对应的梯度值。然后第 3 步直接去应用所有的梯度到所有的 theta 上面。

[[4.23695725]
 [2.84246254]]