分类目录归档：数学

记录学过的数学

【数学基础】python在数学中的简单应用之线性代数基础

发表评论

  线性代数是代数学的一个分支，主要处理线性关系问题(简称先线性问题)。线性代数中的概念是机器学习必备的基础知识，有助于理解不同机器学习算法背后的原理、算法内部是如何运行的，以便在开发机器学习系统时更好地做决策。在机器学习的背景下，线性代数也是一个数学工具，提供了像向量和矩阵这样的数据结构用于组织大量的数据，同时也提供了如加、减、乘、求逆等有助于操作数据的运算，从而将复杂的问题简单化，提升大规模运算的效率。

继续阅读 →

在wordpress中使用latex遇到的问题

发表评论

以下是测试，熟于垃圾数据，请直接看文末总结

就是\(x^{a}\) 的
$$
a \parallel c,b \parallel c \Rightarrow a \parallel b
$$
\( a \parallel c,b \parallel c \Rightarrow a \parallel b \)
$latex a \parallel c,b \parallel c \Rightarrow a \parallel b $
$latex a \parallel c,b \parallel c \Rightarrow a \parallel b $

成功了，舒服了
这里为了避免关键字冲突，影响我要表达的意思，故截图总结说明：
wordpress中使用latex

更新：
如果你用的mathjax插件，直接按照人家语法来就行。
file

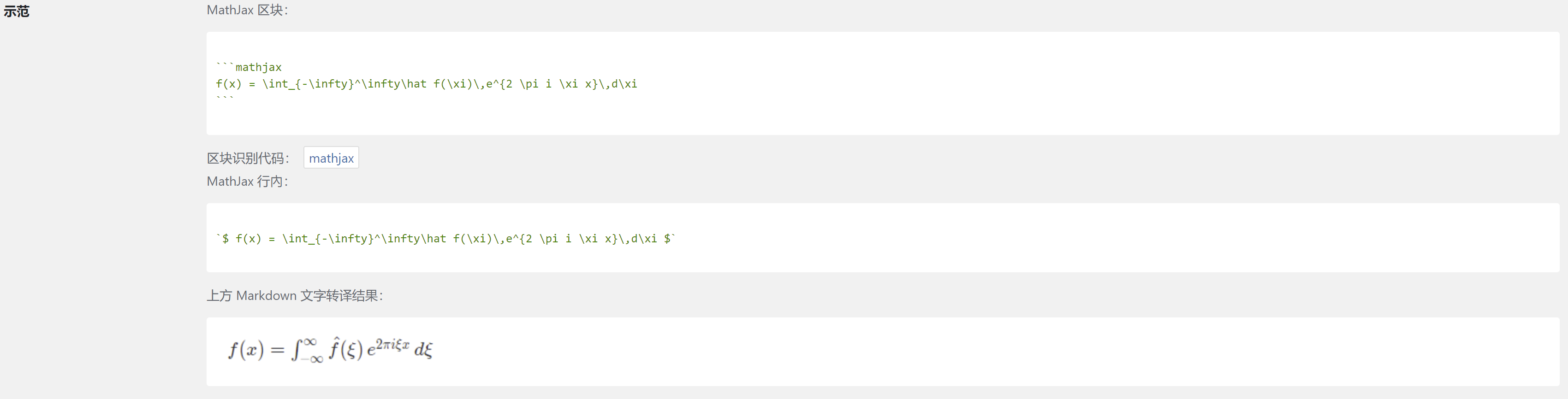
补充：如果latex公式显示异常，可以尝试科学上网后再试。