通过相关分析可以得到两个或两个以上变量之间相关程度及其大小，但对于彼此相关比较紧密的变量，人们总希望建立变量之间具体的数字关系，以便变量之间能够互相推测。回归分析是寻找存在相关关系的变量间的数学表达式并进行统计推断的一种统计方法。相关分析是回归分析的基础和前提，回归分析则是相关分析的深入和继续。

  本文介绍了回归分析的基本理论以及应用python进行回归分析计算和图形绘制的方法。主要内容有回归方程、最小二乘法、一元线性回归、多元线性回归以及曲线线性回归等

  按照自变量的数目，可以分为一元线性回归和多元性先回归；按照自变量和因变量的表现形式，可以分为线性回归和非线性回归。
  一般，回归分析包含四个方向：一元线性回归分析、多元线性回归分析、一元非线性回归分析和多元非线性回归分析。

• 回归分析的一般步骤：
  （1）确定回归方程中的自变量和因变量
  （2）确定回归模型，建立回归方程
  （3）对回归方程进行各种检验
  （4）利用回归方程进行预测

一元线性回归模型

  假设要考虑自变量x和因变量y之间的相关关系，对于自变量x取定一组不完全相同的值x_{1},x_{2},...,x_{n}，做n次独立试验，得到n对观测结果：(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{n},y_{n})，其中y_{i}是x=x_{i}时随机变量Y的观测结果，将n对观测结果（x_{i},y_{i}）,i=1,2,...,n,在直角坐标系中进行描点，这中描点图称为散点图。散点图可以帮助我们组略地看出y与x之间地某种关系。

  y可以看成是由两部分叠加而成，一部分是x的线性函数\beta _{0}+\beta _{1}x，另一部分是随机因素引起的误差\varepsilon，即y=\beta _{0}+\beta _{1}x+\varepsilon
  一般地，如果自变量x和因变量y之间存在如下关系，则可称为一元线性回归模型:

y=\beta _{0}+\beta _{1}x+\varepsilon , \varepsilon \sim N(0,\sigma ^2)

  其中：\beta _{0},\beta _{1}为未知参数，\varepsilon为随机误差，\sigma ^2未知，\beta _{0}称为回归常数，\beta _{1}称为回归系数。

回归方程参数的最小二乘法估计

  一元线性回归模型中\beta _{0},\beta _{1},\sigma ^2为未知参数，如果有n个样本值(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{n},y_{n})这里采用最小二乘法来估计回归系数\beta _{0}和\beta _{1}.
  最小二乘法的基本原则：最优拟合直线应该使各个点到回归直线的距离之和最小，即平方和最小。
另

Q=\sum_{i=1}^{n} (y_{i}-\beta _{0}-\beta _{1}x_{i})^2

  Q是n次观察中误差项\varepsilon _{1}^2之和，称Q为误差平方和，它反映了y和\beta _{0}+\beta _{1}x之间在n次观察中总的误差程度。最小二乘法就是寻找使得Q达到最小值的\hat{\beta } _{0}和\hat{\beta } _{1}作为\beta _{0}和\beta _{1}的点估计。

\sideset {}{}\min_{a,b}Q=\sideset {}{}\min_{a,b}\sum_{i=1}^{n} (y_{i}-\beta _{0}-\beta _{1}x_{i})^2

  上式求出的\hat{\beta } _{0}和\hat{\beta } _{1}称为未知参数\beta _{0}和\beta _{1}的最小二乘法估计。

  下图直观的表示了每个样本点的误差项\varepsilon _{i}为该店到回归直线\hat {y} = \hat \beta _{0} + \hat \beta _{1}x的垂直线长度，即\hat {y}_{i} - \hat \beta _{0} - \hat \beta _{1} x_{i}；总误差项Q表示所有误差项的平方和，在图中对应所有垂直线的长度平方和。用最小二乘法拟合的直线是使得所有垂直偏差的平方和尽可能小的那条直线。

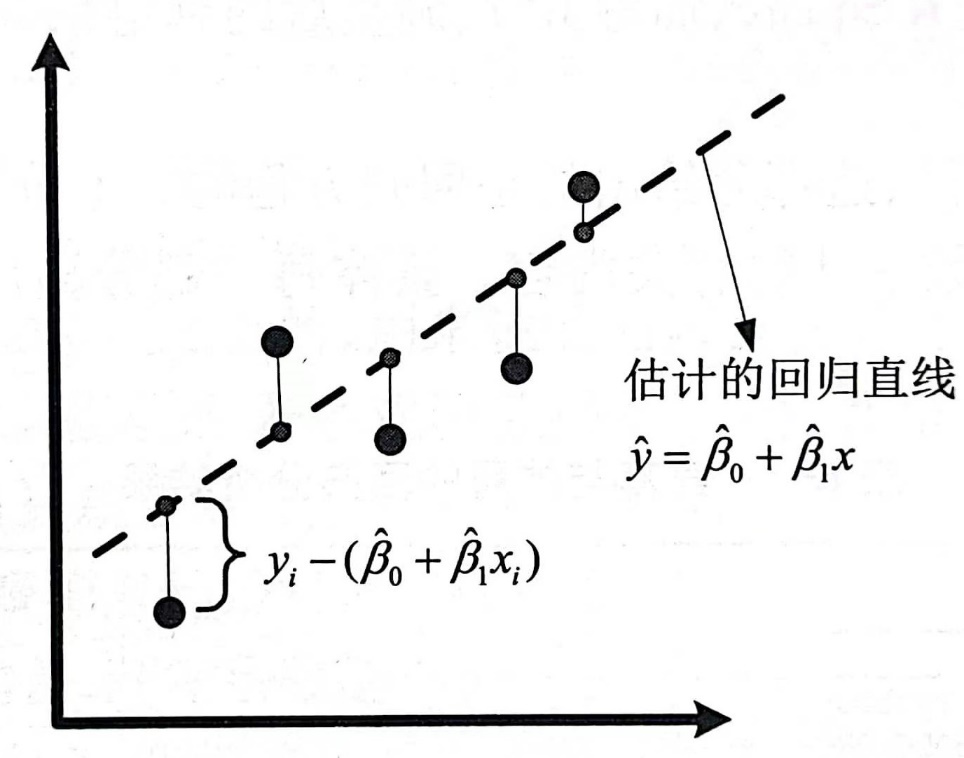
方差的估计

  回归方程y = \beta _{0} + \beta _{1} x+\varepsilon中误差\varepsilon服从N(0,\sigma ^2)，方差\sigma ^2越小，回归方程\hat {y} = \hat \beta _{0} + \hat \beta _{1}x作为y的近似而导致的均方误差就越小。然而方差N(0,\sigma ^2)是未知的，因此需要利用样本去估计N(0,\sigma ^2)。

  记\hat y_{i}=\hat \beta _{0}+\hat \beta _{1}x_{i},i=1,2,...,n,\ y_{i}-\hat y_{i}称为x_{i}处的残差，它表示在x_{i}点大的回归函数值\hat y_{i}和观察值y_{i}的偏差，残差的平方和记为SSE = \sum_{i=1}^{n} (y_{i}-\hat y_{i})^2=\sum_{i=1}^{n}(y _{i} - \hat \beta _{0} - \hat \beta _{1} x_{i})^2

  可以证明\frac{SSE}{\sigma ^2} \sim \mathcal{X}^2(n-2)，又因为卡方分布的期望E[\mathcal{X}^2(n-2)]=n-2，即得\sigma ^2的估计值为\frac{SSE}{n-2}。

  估计方差\sigma ^2越大，则数据点围绕回归直线的分散程度就越大，回归方程的可靠性就越低；估计方差\sigma ^2越小，则数据点围绕回归直线的分散程度就越小，回归方程的代表性越大，可靠性就越高。

为了方便计算，将SSE做如下分解。

SSE = \sum_{i = 1}^{n} (y_{i}-\hat y_{i})^2
=\sum_{i = 1}^{n}[ y_{i}-\bar{y} - \hat{ \beta}_{1}(x_{i}-\bar{x} ) ]^2
=L_{yy}-2 \hat{\beta }_{1}L_{xy}+ \hat{\beta }_{1}^2L_{xx}
=L_{yy}-\hat{\beta }_{1}L_{xy}

得到\hat \sigma ^2的计算公式：L_{yy}-\hat{\beta }_{1}L_{xy}，其中L_{yy}=\sum_{i = 1}^{n} (y_{i}-\bar y_{i})^2=\sum_{i = 1}^{n}y_{i}^2-n\bar{y}^2

多元线性回归模型

  一元线性回归分析中，研究的是因果关系中只涉及某一个因素（自变量）影响另一事物（因变量）的过程，所进行的分析是比较理想化的。但在实际问题中，在线性相关条件下，一个事物（因变量）总是受到其他多种事物（多个自变量）的影响，这时就要使用多元回归分析。此外，许多自变量与因变量之间不存在线性关系，这就要借助于曲线回归分析。
  多元线性回归指的就是多个自变量与一个因变量的线性回归问题。 在现实中，往往会出现数据有多维特征的情况，如有m 个样本，每个样本对应n 维特征和一个结果输出

1. 多元线性回归分析主要解决的问题
   （1）确定几个特定的变量之间是否存在相关关系，如果存在的话，找出它们之间合适的数学表达式。
   （2）根据一个或几个变量的值，解释或预测另一个变量的取值，并且可以知道这种预测或控制能达到什么样的精确度。
   （3）进行因素分析。例如，在共同影响一个变量的许多变量（因素）之间，找出哪些是重要因素，哪些是次要因素，这些因素之间又有什么关系等。

2. 多元线性回归模型
   多元线性回归模型是一元线性回归模型的扩展，其基本原理与一元线性回归模型类似，区别在于影响因素（自变量）更多些，计算上更为复杂，一般需借助计算机来完成。
   
   

3. 多元线性回归模型的参数求解
   
   
   

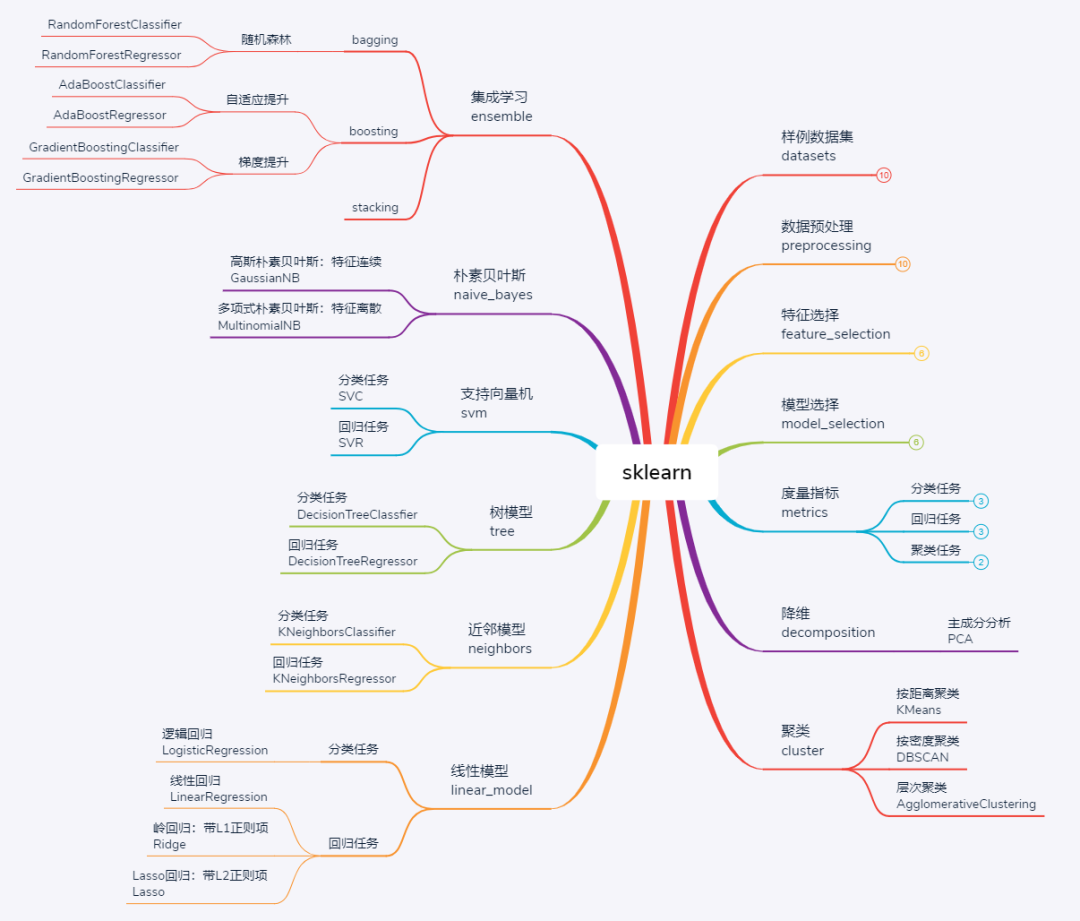
sklearn简介和简单使用

  sklearn，全称scikit-learn，是python中的机器学习库，建立在numpy、scipy、matplotlib等数据科学包的基础之上，涵盖了机器学习中的样例数据、数据预处理、模型验证、特征选择、分类、回归、聚类、降维等几乎所有环节，功能十分强大。与深度学习库存在pytorch、TensorFlow等多种框架可选不同，sklearn是python中传统机器学习的首选库，不存在其他竞争者。
sklearn太强大了，自己对其了解甚少，欲更多了解sklearn，参考[1]

• 编程模拟实现一个简单例子

import numpy as np
import matplotlib.pyplot as plt

X = 2 * np.random.rand(100, 1)  # 生成100行一列的列向量，范围 0-2
y = 5 + 4 * X + np.random.randn(100, 1)  # 模拟生成采集到的的y的样本，通过加一个随机的误差实现

# 前面我们讲过在多元线性回归中，W 的个数其实是和 X 特征的数量一一对应的，比如我们
# 有 X1、X2 两个特征，我们通过多元线性回归就可以求解得到 W1、W2 两个参数，
# 比如我们有 X0、X1 两个特征，我们通过多元线性回归就可以求解得到 W0、W1 两个参数。
# 那么此时我们只有 X1 一列向量，我们还需要一列 X0 才可以去求得 W0，因为我们上面的
# 式子中有个 W0=5 嘛，所以接下来整合 X0 和 X1

X_b = np.c_[np.ones((100, 1)), X]
# 这里的 c_就是拼接，可以把它理解为 concatenate 拼接，而且我们把 X0 一列都设置为 1，
# 这样多元线性回归公式就可以把 1 去乘以 W0，这样就符合公式的定义，还有注意拼接的顺
# 序就是求得对应 W 的顺序

theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
# 这里的.T 就是 transpose 转置的作用，dot 就是向量点乘， np.linalg.inv 是矩阵求逆
# 这个theta_best就是通过对数似然函数推到出来的求最优解的公式，输出为斜率和截距

X_new = np.array([[0],[2]]) 
X_new_b = np.c_[(np.ones((2, 1))), X_new]
print("X_new_b:\n",X_new_b)

y_predict = X_new_b.dot(theta_best)
print("预测值:\n",y_predict)

plt.plot(X_new, y_predict, 'r-')
plt.plot(X, y, 'b.')
plt.axis([0, 2, 0, 15])
plt.show()

X_new_b:
 [[1. 0.]
 [1. 2.]]
预测值:
 [[ 4.85449067]
 [12.62826026]]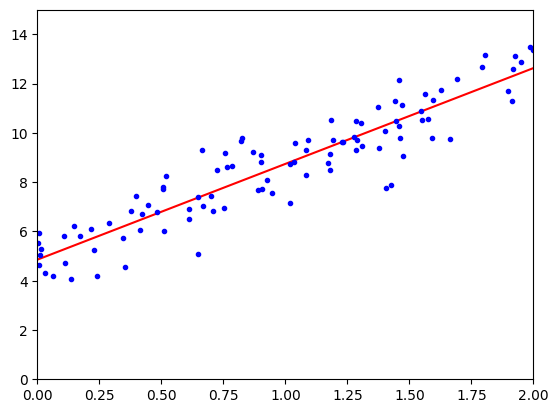

• sklearn调用LinearRegression 类

# 从 sklearn 模块下的线性模块下导入多元线性回归类
import numpy as np
from sklearn.linear_model import LinearRegression

# 构建真实的 X 和 y
X1 = 2 * np.random.rand(100, 1)
X2 = 2 * np.random.rand(100, 1)
X = np.c_[X1, X2]
y = 4 + 3 * X1 + 5 * X2 + np.random.randn(100, 1)

# python 中驼峰原则创建一个类的对象，当然得加上小括号，不过因为是 python 所以不用
# new 关键字，然后把对象赋给一个变量
lin_reg = LinearRegression()

# 接下来，我们去调用 fit 类的方法，这是非常 sklearn 的风格，然后去打印出结果，截距项
# 和参数系数
lin_reg.fit(X, y)

print(lin_reg.intercept_, lin_reg.coef_) # 截距项和参数系数

[4.37345707] [[3.01862964 4.78908486]]

线性回归更多实验：

USA_Housing.csv中包含5000条数据，包括房屋信息、房屋售价等信息，模样如下：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import MaxNLocator
from sklearn.preprocessing import StandardScaler

# 从源文件加载数据，并输出查看数据的各项特征
lines = np.loadtxt('USA_Housing.csv', delimiter=',', dtype='str')
header = lines[0]
lines = lines[1:].astype(float)
print('数据特征：', ', '.join(header[:-1]))
print('数据标签：', header[-1])
print('数据总条数：', len(lines))

# 划分训练集与测试集
ratio = 0.8
split = int(len(lines) * ratio)
np.random.seed(0)
lines = np.random.permutation(lines)
train, test = lines[:split], lines[split:]

# 数据归一化
scaler = StandardScaler()
scaler.fit(train) # 只使用训练集的数据计算均值和方差
train = scaler.transform(train)
test = scaler.transform(test)

# 划分输入和标签
x_train, y_train = train[:, :-1], train[:, -1].flatten()
x_test, y_test = test[:, :-1], test[:, -1].flatten()

数据特征： Avg. Area Income, Avg. Area House Age, Avg. Area Number of Rooms, Avg. Area Number of Bedrooms, Area Population
数据标签： Price
数据总条数： 5000

# 在X矩阵最后添加一列1，代表常数项
X = np.concatenate([x_train, np.ones((len(x_train), 1))], axis=-1)
# @ 表示矩阵相乘，X.T表示矩阵X的转置，np.linalg.inv函数可以计算矩阵的逆
theta = np.linalg.inv(X.T @ X) @ X.T @ y_train
print('回归系数：', theta)

# 在测试集上使用回归系数进行预测
X_test = np.concatenate([x_test, np.ones((len(x_test), 1))], axis=-1)
y_pred = X_test @ theta

# 计算预测值和真实值之间的RMSE（均方根误差）
rmse_loss = np.sqrt(np.square(y_test - y_pred).mean())
print('RMSE：', rmse_loss)

回归系数： [ 6.50881254e-01  4.67222833e-01  3.38466198e-01  6.17275856e-03
  4.26857089e-01 -1.46033359e-14]
RMSE： 0.28791834247503534

from sklearn.linear_model import LinearRegression

# 初始化线性模型
linreg = LinearRegression()
# LinearRegression的方法中已经考虑了线性回归的常数项，所以无须再拼接1
linreg.fit(x_train, y_train)

# coef_是训练得到的回归系数，intercept_是常数项
print('回归系数：', linreg.coef_, linreg.intercept_)
y_pred = linreg.predict(x_test)

# 计算预测值和真实值之间的RMSE
rmse_loss = np.sqrt(np.square(y_test - y_pred).mean())
print('RMSE：', rmse_loss)

回归系数： [0.65088125 0.46722283 0.3384662  0.00617276 0.42685709] -1.4635041882766192e-14
RMSE： 0.2879183424750354

梯度下降算法

# 该函数每次返回大小为batch_size的批量
# x和y分别为输入和标签
# 若shuffle = True，则每次遍历时会将数据重新随机划分
def batch_generator(x, y, batch_size, shuffle=True):
    # 批量计数器
    batch_count = 0
    if shuffle:
        # 随机生成0到len(x)-1的下标
        idx = np.random.permutation(len(x))
        x = x[idx]
        y = y[idx]
    while True:
        start = batch_count * batch_size
        end = min(start + batch_size, len(x))
        if start >= end:
            # 已经遍历一遍，结束生成
            break
        batch_count += 1
        yield x[start: end], y[start: end]

def SGD(num_epoch, learning_rate, batch_size):
    # 拼接原始矩阵
    X = np.concatenate([x_train, np.ones((len(x_train), 1))], axis=-1)
    X_test = np.concatenate([x_test, np.ones((len(x_test), 1))], axis=-1)
    # 随机初始化参数
    theta = np.random.normal(size=X.shape[1])

    # 随机梯度下降
    # 为了观察迭代过程，我们记录每一次迭代后在训练集和测试集上的均方根误差
    train_losses = []
    test_losses = []
    for i in range(num_epoch):
        # 初始化批量生成器
        batch_g = batch_generator(X, y_train, batch_size, shuffle=True)
        train_loss = 0
        for x_batch, y_batch in batch_g:
            # 计算梯度
            grad = x_batch.T @ (x_batch @ theta - y_batch)
            # 更新参数
            theta = theta - learning_rate * grad / len(x_batch)
            # 累加平方误差
            train_loss += np.square(x_batch @ theta - y_batch).sum()
        # 计算训练和测试误差
        train_loss = np.sqrt(train_loss / len(X))
        train_losses.append(train_loss)
        test_loss = np.sqrt(np.square(X_test @ theta - y_test).mean())
        test_losses.append(test_loss)

    # 输出结果，绘制训练曲线
    print('回归系数：', theta)
    return theta, train_losses, test_losses

# 设置迭代次数，学习率与批量大小
num_epoch = 20
learning_rate = 0.01
batch_size = 32
# 设置随机种子
np.random.seed(0)

_, train_losses, test_losses = SGD(num_epoch, learning_rate, batch_size)

# 将损失函数关于运行次数的关系制图，可以看到损失函数先一直保持下降，之后趋于平稳
plt.plot(np.arange(num_epoch), train_losses, color='blue', 
    label='train loss')
plt.plot(np.arange(num_epoch), test_losses, color='red', 
    ls='--', label='test loss')
# 由于epoch是整数，这里把图中的横坐标也设置为整数
# 该步骤也可以省略
plt.gca().xaxis.set_major_locator(MaxNLocator(integer=True))
plt.xlabel('Epoch')
plt.ylabel('RMSE')
plt.legend()
plt.show()

回归系数： [ 0.65357756  0.46682964  0.33885411  0.00720843  0.42751035 -0.00273407]

学习率

_, loss1, _ = SGD(num_epoch=num_epoch, learning_rate=0.1, 
    batch_size=batch_size)
_, loss2, _ = SGD(num_epoch=num_epoch, learning_rate=0.001, 
    batch_size=batch_size)
plt.plot(np.arange(num_epoch), loss1, color='blue', 
    label='lr=0.1')
plt.plot(np.arange(num_epoch), train_losses, color='red', 
    ls='--', label='lr=0.01')
plt.plot(np.arange(num_epoch), loss2, color='green',
    ls='-.', label='lr=0.001')
plt.xlabel('Epoch')
plt.ylabel('RMSE')
plt.gca().xaxis.set_major_locator(MaxNLocator(integer=True))
plt.legend()
plt.show()

回归系数： [0.64542258 0.47047873 0.33188398 0.00325404 0.42479699 0.00237965]
回归系数： [0.59247915 0.58561574 0.26554358 0.10173112 0.49435997 0.13108641]

_, loss3, _ = SGD(num_epoch=num_epoch, learning_rate=1.5, batch_size=batch_size)
print('最终损失：', loss3[-1])
plt.plot(np.arange(num_epoch), np.log(loss3), color='blue', label='lr=1.5')
plt.xlabel('Epoch')
plt.ylabel('log RMSE')
plt.gca().xaxis.set_major_locator(MaxNLocator(integer=True))
plt.legend()
plt.show()

回归系数： [ 1.02026986e+76 -1.13520942e+76  9.19402885e+75  5.66309332e+75
 -4.91083973e+75  5.35399839e+75]
最终损失： 5.336762494108163e+77