内容目录
SVM 源于统计学理论,基于 VC 维理论和结构风险最小原理,根据有限的样本信息在模型的复杂性(即对特定训练样本的学习精度)和学习能力(即无错误地识别任意样本的能力)之间寻求最佳折中,以期获得最好的推广能力(或称泛化能力)。统计机器学习能够精确地给出学习效果以 及解答需要的样本数等一系列问题。所谓 VC 维是对函数类的一种度量,可以简单地理解为问题的复杂程度。VC 维越高,问题越复杂。SVM 的基本模型是二类分类模型,属于有监督学习,是在特征空间中找出一个超平面作为分类边界,对数据进行正确分类,且使每一类样本中距离分类边界最近的样本到分类边界的距离尽可能远,使分类误差最小化。
# 小试牛刀(svm线性分类)
import numpy as np
from sklearn.svm import SVC
#导入数据
# 3个测试数据
x = np.array([[4,3],[3,3],[1,1]])
y = np.array([1,1,-1])
print("训练集(最后一列为标签):\n",np.hstack((x,y.reshape(3,1))))
# 调用SVC,训练算法
model = SVC(kernel="linear") # 实例化,设置的核函数为线性核函数
model.fit(x,y) # 训练模型,和上一句配合使用
# 预测数据
predict_val = model.predict([[4,5],[0,0],[1,3]])
print("预测数据[4,5],[0,0],[1,3]的类型值分别是:", predict_val)
# 相关方法和返回值
w = model.coef_[0] # 获取w
a = -w[0]/w[1] # 斜率
print("支持向量:\n", model.support_vectors_) # 输出支持向量
print("支持向量的标号:\n",model.support_) # 输出支持向量的标号
print("每类支持向量的个数:", model.n_support_) # 每类支持向量的个数
print("数据集X到分类超平面的距离:", model.decision_function(x))
print("参数(法向量)w=",w)
print("分类线的斜率a=",a)
print("分类平面截距b:", model.intercept_) # 超平面的截距值(常数值)
print("系数:", model.coef_) # 每个特征系数(重要性),只有linearSVC核函数可用训练集(最后一列为标签):
[[ 4 3 1]
[ 3 3 1]
[ 1 1 -1]]
预测数据[4,5],[0,0],[1,3]的类型值分别是: [ 1 -1 1]
支持向量:
[[1. 1.]
[3. 3.]]
支持向量的标号:
[2 1]
每类支持向量的个数: [1 1]
数据集X到分类超平面的距离: [ 1.5 1. -1. ]
参数(法向量)w= [0.5 0.5]
分类线的斜率a= -1.0
分类平面截距b: [-2.]
系数: [[0.5 0.5]]# 非线性SVM实现分类,分别使用线性核、多项式核核高斯径向基核实现,并作对比
# 通过plot_decision_boundary()函数实现散点图和支持向量的绘图
import numpy as np
from sklearn.svm import SVC
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles # 画圆圈的库
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
# 画分类数据集
def plot_decision_boundary(model,X,y,h=0.03,draw_SV=True,title='decision_boundary'):
X_min,X_max = X[:,0].min()-1,X[:,0].max()+1
y_min,y_max = X[:,1].min()-1,X[:,1].max()+1
# 画决策边界,需要有网格,利用np.meshgrid()函数生成一个坐标矩阵
xx,yy = np.meshgrid(np.arange(X_min,X_max,h),np.arange(y_min,y_max,h))
# 预测坐标矩阵中每个点所属的类别
label_predict = model.predict(np.stack((xx.flat,yy.flat),axis=1))
# 将结果放入彩色图中
label_predict = label_predict.reshape(xx.shape) # 使之与输入的形状相同
plt.title(title)
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
plt.xticks(())
plt.yticks(())
plt.contourf(xx,yy,label_predict,alpha=0.5)
# 用contourf()函数为坐标矩阵中不同类别填充不同颜色
markers = ['x','^','o']
colors = ['b','r','c']
classes = np.unique(y)
# 画出每一类数据的散点图
for label in classes:
plt.scatter(X[y==label][:,0],X[y==label][:,1],c=colors[label],s=60,marker=markers[label])
# 标记出支持向量,将两类支持向量用不同颜色表示出来
if draw_SV:
SV = model.support_vectors_ # 获取支持向量
n = model.n_support_[0] # 第一类支持向量个数
plt.scatter(SV[:n,0],SV[:n,1],s=15,c='black',marker='o')
plt.scatter(SV[n:,0],SV[n:,1],s=15,c='g',marker='o')# 生成两个特性、两个类别的数据集,并画出来
X,y = make_circles(200,factor=0.1,noise=0.1) # 产生样本点
plt.scatter(X[y==0,0],X[y==0,1],c='b',s=20,marker='x')
plt.scatter(X[y==1,0],X[y==1,1],c='r',s=20,marker='^')
plt.xticks(())
plt.yticks(())
plt.title("数据集")
plt.show()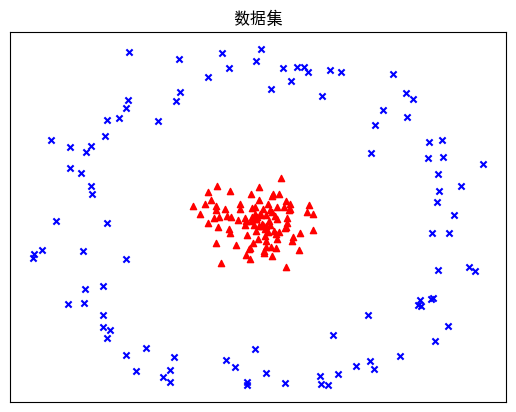
# 分别构造线性核函数和三阶多项式核函数的SVM,把运算的结果用图形绘制
# svm软间隔分类使用到了一个惩罚系数C
# 当C趋近于无穷大时,意味着分类严格不能有错误,分类间隔越小
# 当C趋近于很小时,意味着可以有更大的错误容忍度,分类间隔越小,本例设置C=1
# 多项式核函数的参数为d=3,C=1,γ=0.5
plt.figure(figsize=(12,10),dpi=200)
# 使用线性核函数进行分类
model_linear = SVC(C=1,kernel='linear') # 实例化,设置的核函数为线性核函数
model_linear.fit(X,y) # 用训练集数据训练模型,和上一句配合使用
# 画出使用线性核函数的分类边界
plt.subplot(2,2,1)
plot_decision_boundary(model_linear,X,y,title='线性核函数') # 调用函数画图
print("采用线性核函数生成的支持向量个数:", model_linear.n_support_)
# 使用多项式核函数进行分类
# 实例化,设置的核函数为多项式核函数
model_poly = SVC(C=1.0,kernel='poly',degree=3,gamma="auto")
model_poly.fit(X,y) # 训练
# 画出使用多项式核函数的分类边界
plt.subplot(2,2,2)
plot_decision_boundary(model_poly,X,y,title='多项式核函数') # 调用函数画图
print("采用多项式核函数生成的支持向量个数:", model_poly.n_support_)
plt.show()采用线性核函数生成的支持向量个数: [100 100]
采用多项式核函数生成的支持向量个数: [100 100]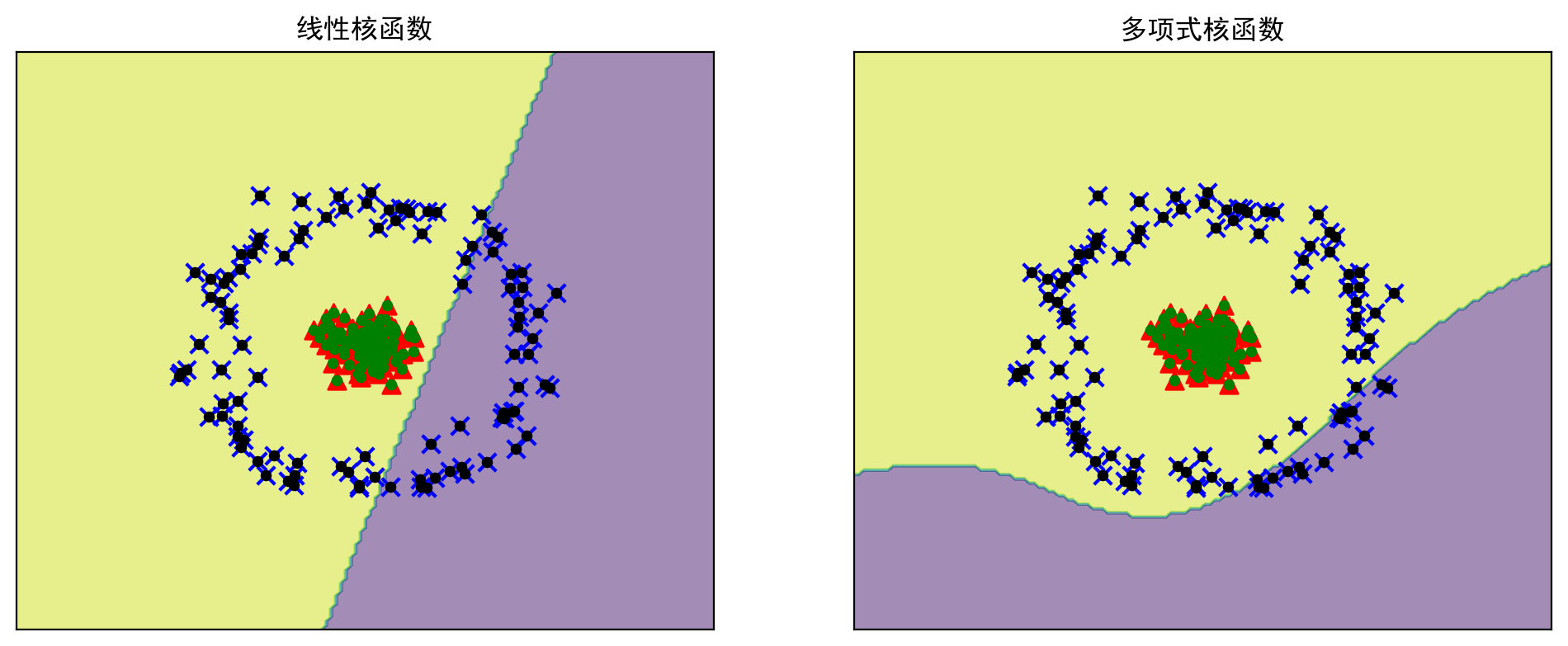
# 可以看出,线性核函数和多项式核函数的所有样本均是支持向量,显然在此问题上不适用# 下面调用SVC(), 分别构建四个高斯径向基核函数的SVM,对应的γ分别为10,1,0.1,0.01
plt.figure(figsize=(12,10),dpi=200)
for j,gamma in enumerate((10,1,0.1,0.01)):
plt.subplot(2,2,j+1)
mode_rbf = SVC(C=1.0,kernel='rbf',gamma=gamma)
mode_rbf.fit(X,y)
plot_decision_boundary(mode_rbf,X,y,title=f"rbf函数,参数γ={gamma}")
print(f"rbf函数,参数γ={gamma},支持向量个数:{mode_rbf.n_support_}")
plt.show()rbf函数,参数γ=10,支持向量个数:[34 7]
rbf函数,参数γ=1,支持向量个数:[12 10]
rbf函数,参数γ=0.1,支持向量个数:[95 94]
rbf函数,参数γ=0.01,支持向量个数:[100 100]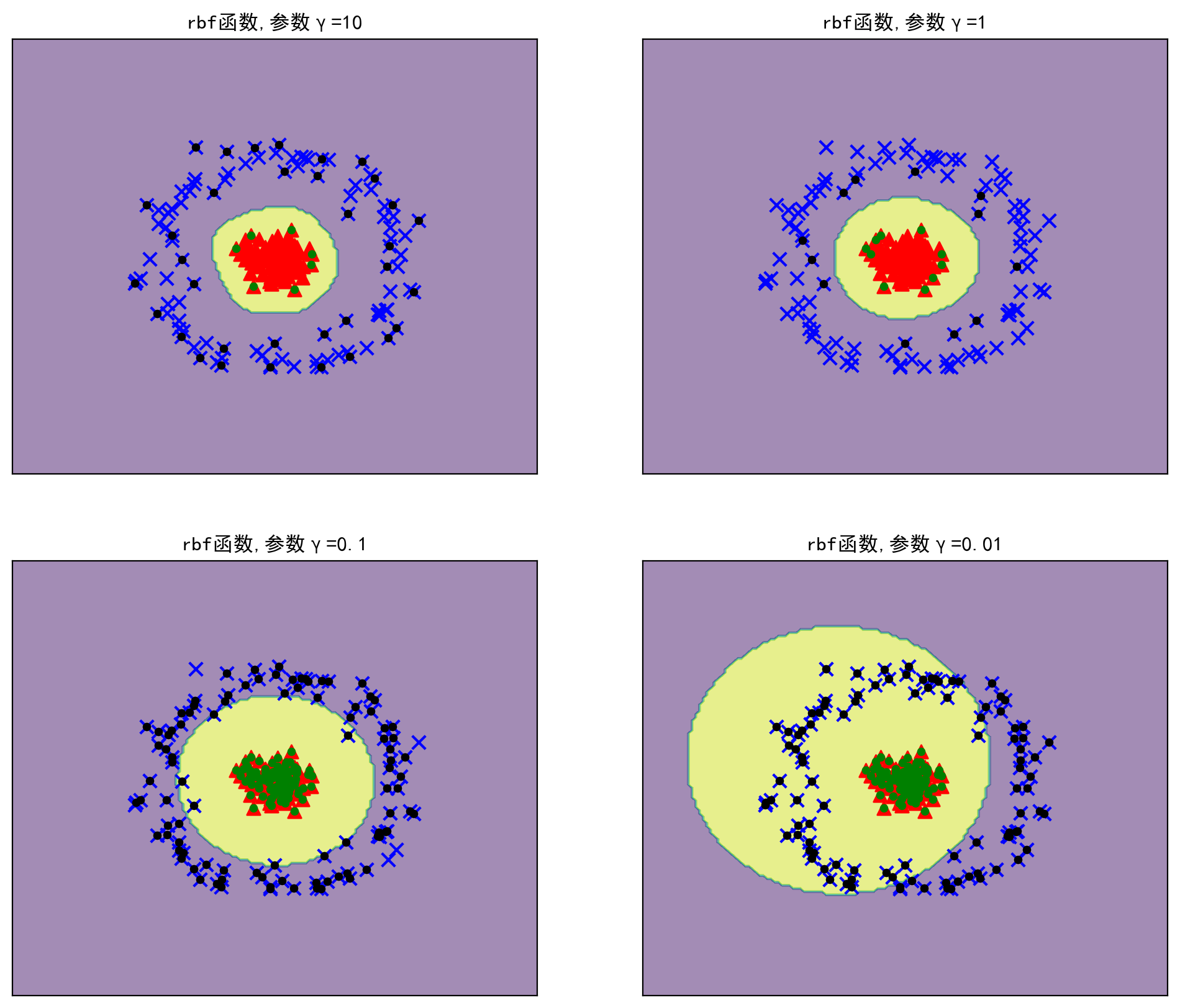
# 结果显示,高斯径向基核函数能将这两类进行很好的分类。在γ为1时,只用了22个支持向量,
# 边界曲线可以较好地拟合数据集特点# 通过上面的实验我们发现使用多项式核函数、高斯径向基核函数的SVM确实可以解决部分非线性
# 可分问题。不同的参数对精度的影响非常大,一般来说,C越大,训练得到的模型越准确。
# 如果采用高斯径向基核函数,参数的值对精度影响也非常大,参数的值越大,分类模型越准确。
# 因此,在实际应用时调一组好的参数非常重要# 引申
# sklearn提供了GridSearchCV()函数,实现自动调参,把参数输入进去,就能给出最优的结果和参数。
# 通过对线性核函数、多项式核函数和高斯径向基核函数使用网格搜索,在C=(0.1,1,10)和
# gamma=(1,0.1,0.01)形成的9种情况种选择最好的超参数
from sklearn.model_selection import GridSearchCV
tuned_parameters = [{'kernel': ['rbf'],'gamma': [1,0.1,0.01], 'C': [0.1,1,10]},
{'kernel': ['linear'], 'C': [0.1,1,10]},
{'kernel': ['poly'],'gamma': [1,0.1,0.01], 'C': [0.1,1,10]},
]
model_grid = GridSearchCV(SVC(),tuned_parameters,cv=5)
model_grid.fit(X,y)
print(f"The best parameters are {model_grid.best_params_} with a score of {model_grid.best_score_}")The best parameters are {'C': 0.1, 'gamma': 1, 'kernel': 'rbf'} with a score of 1.0