线性代数是代数学的一个分支，主要处理线性关系问题(简称先线性问题)。线性代数中的概念是机器学习必备的基础知识，有助于理解不同机器学习算法背后的原理、算法内部是如何运行的，以便在开发机器学习系统时更好地做决策。在机器学习的背景下，线性代数也是一个数学工具，提供了像向量和矩阵这样的数据结构用于组织大量的数据，同时也提供了如加、减、乘、求逆等有助于操作数据的运算，从而将复杂的问题简单化，提升大规模运算的效率。

向量

  向量是线性代数最基础、最根源的组成部分，也是机器学习的基础数据表示形式。机器学习中的投影、降维等概念，都是在向量的基础上实现的。

• 向量的定义（略）
• 向量的基本运算：加法和数乘（略）
• 向量与数据
    在机器学习中，对一个对象或事件的描述称为样本，反映样本某方面的表现或性质的事项称为特征或属性，特征的取值称为特征值，由样本组成的集合称为数据集。在数据集中，样本用向量表示，向量的维度可以看作样本的特征数。如经典的鸢尾花数据集，用萼片长度、萼片宽度、花瓣长度和花瓣宽度4 个特征刻画鸢尾花，4 个特征值组成一个样本，用四维行向量表示。如一个行向量[5.1,3.5,1.4,0.2] 表示一个鸢尾花样本，则有5.1、3.5、1.4 和0.2 共4 个特征值。

矩阵

  标量是一个数，向量是对标量的扩展，是一组数；矩阵是对向量的扩展，可看作一组向量。在图像处理、人工智能等领域，常用矩阵来表示和处理大量的数据。矩阵是线性代数中最有用的工具。

• 矩阵的定义（略）
  从数组的角度看，向量是一维数组，是标量的数组；矩阵是二维数组，是向量的数组。
• 矩阵和数据
  矩阵的外观就是长方形的数表，生活中一些长方形的数表也可以看作矩阵，矩阵在日常生活、科学计算及机器学习中应用广泛。

例1：

  生活中对象之间的关系常用表格表示。例如有 A、B、C、D共4个城市，它们之间的通行关系如下所示，习惯上用表格表示该图，行和列分别代表四个城市，用对号“√”表示两个城市可以通行。计算机中可以用矩阵表示，行和列分别代表四个城市，使用0、1分别代表两个城市不可通行和可通行关系，下表对应的矩阵为A。

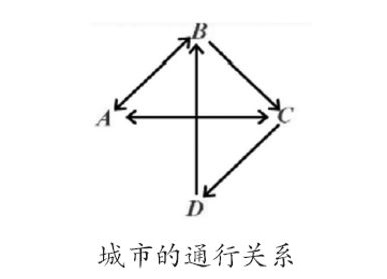
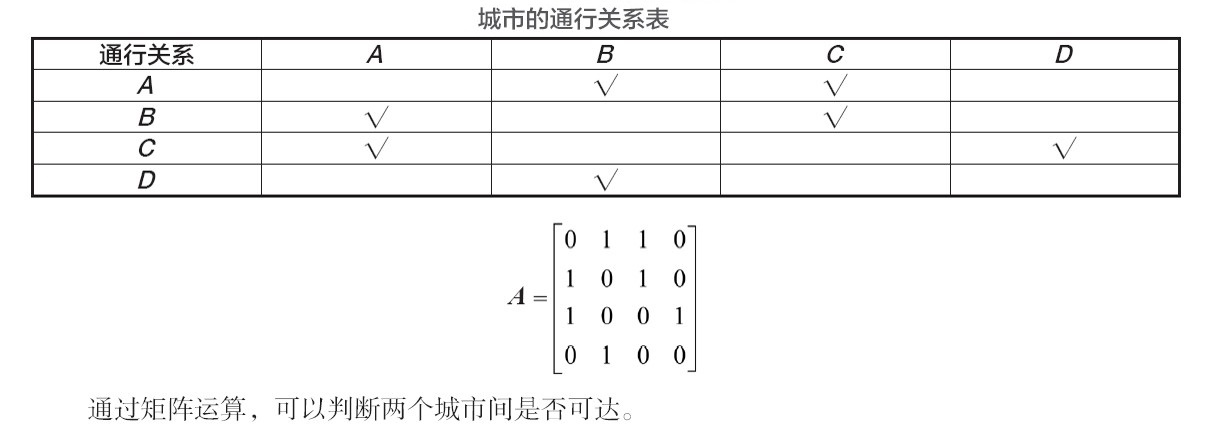
例2：

  在机器学习中，样本集合(也称为数据集)常用矩阵表示，每行数据称为一个样本(或个数据对象)，每列表达样本的一个特征(属性)或者标记，例如下表的鸢尾花数据集，每行代表一个样本。前四列分别代表一个特征，最后一列是标记，表示所属类别。该数据集可以用矩阵A表示。