【数学基础】python在数学中的简单应用之高数基础

发表评论
内容目录

对于大家大学期间都学过的数学理论知识，这里可能摘录较少，但会用python代码去实现一些常见计算；对于本人之前不太理解或者和机器学习算法密切相关的知识，会记录多一些。

  • 极限的计算
  1. 使用python编程计算 \(\lim_{x \to \infty} \frac{\sin x} {x}\)
# 计算极限

import sympy
from sympy import oo # 注意无穷符号表现形式为两个小写字母oo
import numpy as np

x = sympy.Symbol('x') # 注意Symbol首写字母大写
f = sympy.sin(x)/x
sympy.limit(f,x,oo)

    0
  1. 使用python编程计算limx→1x2−1x−1
import sympy
import numpy as pd

x = sympy.Symbol('x')
f = (x**2 - 1)/(x - 1)
sympy.limit(f,x,1)
    2
  • 函数求导
    1. 求函数y=arcsin⁡sin⁡x
      的导数，并用python编程求导。

解：

y′=11−(sin⁡x)2(sin⁡x)′=11−(sin⁡x)∙12sin⁡x∙(sin⁡x)′=cos⁡x2sin⁡x(1−sin⁡x)

使用python编程求解
# diff是求导函数方法
# arcsin数学函数表现形式为asin

from sympy import *
from sympy.abc import x,y,z,f

diff(asin(sqrt(sin(x))))

  • 函数求偏导
  1. 求f(x,y)=x2+3xy+y2在点（1，2）处的偏导数，并用python编程实现。

解：

fx(x,y)=2x+3y
fy(x,y)=3x+2y
fx(1,2)=2x+3y|y=2x=1=8
fy(1,2)=3x+2y|y=2x=1=7

python代码求解：

from sympy import *
from sympy.abc import x,y,z,f

f = x**2 + 3*x*y + y**2

fx = diff(f,x)
fy = diff(f,y)
display(fx)  # jupyter notebook里面的display和python本身的print函数区别不大
display(fy)


fx.evalf(subs={x:1,y:2})
    8.0
fy.evalf(subs={x:1,y:2})
    7.0
  • 方向导数与梯度
    案例：梯度下降法求函数最小值

      梯度下降法，是寻找函数极小值常用的优化方法。当目标函数是凸函数时，梯度下降法的解是全局解。但在一般情况下，其解不保证是全局最优解。最普遍的做法就是，在已知参数当前值时，按当前点对应的梯度向量的反方向及事先定好的步长大小对参数进行调整。按上述方法对参数做出多次调整之后，函数就会逼近一个极小值。
      例如，假设函数f(x)为一元连续函数,初始值为\(x_{0}\)，\(\alpha\) 为步长，已知在点\(x_{0}\)的梯度为\(gard\ f(x_{0})\)，那么下一个点的坐标为\(x_{1}=x_{0}-\alpha\ast gard\ f(x_{0})\)，然后再求点\(x_{1}\)的梯度，反复迭代，直到\(f(x_{n})-f(x_{n-1})\)的绝对差极小，迭代结束，此时\(f(x_{n})\)即为极小值。

  • 例子：应用python编程实现梯度下降法求解下面函数的最小值，并使用matplotlib、mpl_toolkits库画出函数的图形。
    \(min\ f(x) = x_{1}-x_{2}+2x_{1}^2+2x_{1}x_{2}+x_{2}^2\)，给定初始值\(X^{(0)}=(0,0)^{T}\)
    解：
    matplotlib.pyplot是是个有命令风格的函数集合，他看起来和MATLAB很相似，每一个pyplot函数都使一幅图像figure做出些许改变mpl_toolkits.mplot3d是三维绘图工具包。
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
def Fun(x,y):
    return x-y+2*x*x+2*x*y+y*y

def PxFun(x,y): # 求x偏导
    return 1+4*x+2*y
def PyFun(x,y): # 求y偏导
    return -1+2*x+2*y

fig = plt.figure() # figure对象
ax = fig.add_subplot(projection='3d') # figure.add_subplot(projection='3d')
X,Y = np.mgrid[-2:2:40j,-2:2:40j] # 取样并作满射联合
Z = Fun(X,Y) # 取样表Z坐标打表

ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap="rainbow")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')

# 梯度下降
step= 0.0008 # 取步长

x = 0
y = 0
tag_x = [x]
tag_y = [y]
tag_z = [Fun(x,y)]

new_x = x
new_y = y
Over = False
while Over == False:
    new_x -= step * PxFun(x,y)
    new_y -= step * PyFun(x,y)

    if Fun(x,y) - Fun(new_x,new_y) < 7e-9:
        Over = True
    x = new_x
    y = new_y
    tag_x.append(x)
    tag_y.append(y)
    tag_z.append(Fun(x,y))

ax.plot(tag_x,tag_y,tag_z,'r')
plt.title('(x,y)~(' + str(x) + "," + str(y) + ")")
plt.show()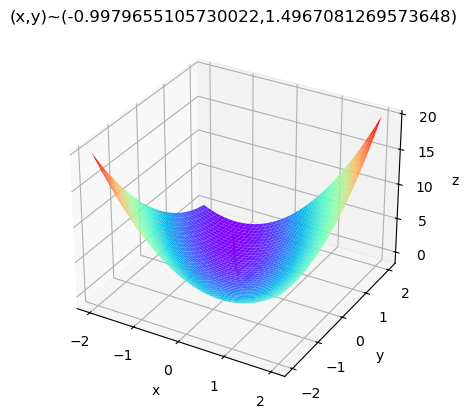

png

由图上显示所求解为\(x\approx -0.9979, y\approx 1.4967\)

发表回复